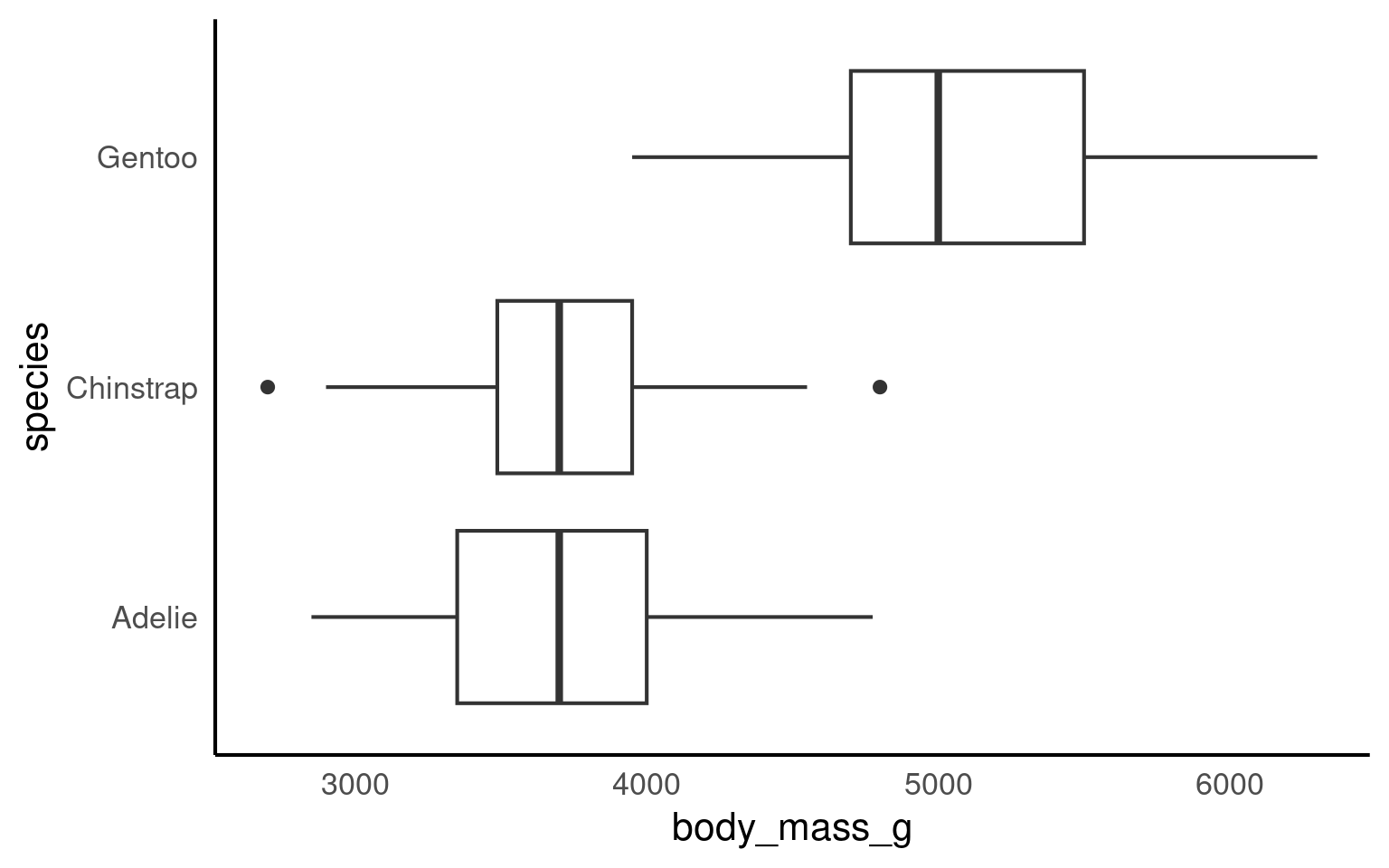16  Data insights

16.1 Learning Objectives

  • Use summary functions to explore the structure and completeness of a dataset.

  • Create simple summaries and grouped summaries using count(), group_by(), and summarise().

  • Calculate descriptive statistics (mean, SD) across groups.

  • Use janitor tools Firke (2024) to quickly tabulate and summarise categorical data.

  • Recognise how grouping can change the interpretation of summaries and relationships

16.2 A first glimpse

When starting with a new dataset, we want to get an initial idea:

  • How many rows and columns are there?

  • What are the column names?

  • What types of data are in each column?

  • What are their possible values or ranges?

  • These answers are useful to know before jumping into wrangling and cleaning data.

There are several ways to return an overview of your data, ranging in how comprehensively you wish to summarise your data’s structure.

16.3 The data

penguins <- read_csv(here("data", "penguins_clean.csv"))
glimpse(penguins)
Rows: 344
Columns: 19
$ study_name        <chr> "PAL0708", "PAL0708", "PAL0708", "PAL0708", "PAL0708…
$ sample_number     <dbl> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1…
$ species           <chr> "Adelie", "Adelie", "Adelie", "Adelie", "Adelie", "A…
$ region            <chr> "Anvers", "Anvers", "Anvers", "Anvers", "Anvers", "A…
$ island            <chr> "Torgersen", "Torgersen", "Torgersen", "Torgersen", …
$ stage             <chr> "Adult, 1 Egg Stage", "Adult, 1 Egg Stage", "Adult, …
$ individual_id     <chr> "N1A1", "N1A2", "N2A1", "N2A2", "N3A1", "N3A2", "N4A…
$ clutch_completion <chr> "Yes", "Yes", "Yes", "Yes", "Yes", "Yes", "No", "No"…
$ date_egg          <date> 2007-11-11, 2007-11-11, 2007-11-16, 2007-11-16, 200…
$ culmen_length_mm  <dbl> 39.1, 39.5, 40.3, NA, 36.7, 39.3, 38.9, 39.2, 34.1, …
$ culmen_depth_mm   <dbl> 18.7, 17.4, 18.0, NA, 19.3, 20.6, 17.8, 19.6, 18.1, …
$ flipper_length_mm <dbl> 181, 186, 195, NA, 193, 190, 181, 195, 193, 190, 186…
$ body_mass_g       <dbl> 3750, 3800, 3250, NA, 3450, 3650, 3625, 4675, 3475, …
$ sex               <chr> "Male", "Female", "Female", NA, "Female", "Male", "F…
$ delta_15_n_o_oo   <dbl> NA, 8.94956, 8.36821, NA, 8.76651, 8.66496, 9.18718,…
$ delta_13_c_o_oo   <dbl> NA, -24.69454, -25.33302, NA, -25.32426, -25.29805, …
$ comments          <chr> "Not enough blood for isotopes.", NA, NA, "Adult not…
$ year              <dbl> 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007, 2007…
$ mass_range        <fct> mid penguin, mid penguin, smol penguin, NA, smol pen…
str(penguins)
tibble [344 × 19] (S3: tbl_df/tbl/data.frame)
 $ study_name       : chr [1:344] "PAL0708" "PAL0708" "PAL0708" "PAL0708" ...
 $ sample_number    : num [1:344] 1 2 3 4 5 6 7 8 9 10 ...
 $ species          : chr [1:344] "Adelie" "Adelie" "Adelie" "Adelie" ...
 $ region           : chr [1:344] "Anvers" "Anvers" "Anvers" "Anvers" ...
 $ island           : chr [1:344] "Torgersen" "Torgersen" "Torgersen" "Torgersen" ...
 $ stage            : chr [1:344] "Adult, 1 Egg Stage" "Adult, 1 Egg Stage" "Adult, 1 Egg Stage" "Adult, 1 Egg Stage" ...
 $ individual_id    : chr [1:344] "N1A1" "N1A2" "N2A1" "N2A2" ...
 $ clutch_completion: chr [1:344] "Yes" "Yes" "Yes" "Yes" ...
 $ date_egg         : Date[1:344], format: "2007-11-11" "2007-11-11" ...
 $ culmen_length_mm : num [1:344] 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42 ...
 $ culmen_depth_mm  : num [1:344] 18.7 17.4 18 NA 19.3 20.6 17.8 19.6 18.1 20.2 ...
 $ flipper_length_mm: num [1:344] 181 186 195 NA 193 190 181 195 193 190 ...
 $ body_mass_g      : num [1:344] 3750 3800 3250 NA 3450 ...
 $ sex              : chr [1:344] "Male" "Female" "Female" NA ...
 $ delta_15_n_o_oo  : num [1:344] NA 8.95 8.37 NA 8.77 ...
 $ delta_13_c_o_oo  : num [1:344] NA -24.7 -25.3 NA -25.3 ...
 $ comments         : chr [1:344] "Not enough blood for isotopes." NA NA "Adult not sampled." ...
 $ year             : num [1:344] 2007 2007 2007 2007 2007 ...
 $ mass_range       : Factor w/ 3 levels "smol penguin",..: 2 2 1 NA 1 2 2 3 1 2 ...
library(skimr)

skim(penguins)
Data summary
Name penguins
Number of rows 344
Number of columns 19
_______________________
Column type frequency:
character 9
Date 1
factor 1
numeric 8
________________________
Group variables None

Variable type: character

skim_variable n_missing complete_rate min max empty n_unique whitespace
study_name 0 1.00 7 7 0 3 0
species 0 1.00 6 9 0 3 0
region 0 1.00 6 6 0 1 0
island 0 1.00 5 9 0 3 0
stage 0 1.00 18 18 0 1 0
individual_id 0 1.00 4 6 0 190 0
clutch_completion 0 1.00 2 3 0 2 0
sex 11 0.97 4 6 0 2 0
comments 290 0.16 18 68 0 10 0

Variable type: Date

skim_variable n_missing complete_rate min max median n_unique
date_egg 0 1 2007-11-09 2009-12-01 2008-11-09 50

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
mass_range 2 0.99 FALSE 3 mid: 146, cho: 118, smo: 78

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
sample_number 0 1.00 63.15 40.43 1.00 29.00 58.00 95.25 152.00 ▇▇▆▅▃
culmen_length_mm 2 0.99 43.92 5.46 32.10 39.23 44.45 48.50 59.60 ▃▇▇▆▁
culmen_depth_mm 2 0.99 17.15 1.97 13.10 15.60 17.30 18.70 21.50 ▅▅▇▇▂
flipper_length_mm 2 0.99 200.92 14.06 172.00 190.00 197.00 213.00 231.00 ▂▇▃▅▂
body_mass_g 2 0.99 4201.75 801.95 2700.00 3550.00 4050.00 4750.00 6300.00 ▃▇▆▃▂
delta_15_n_o_oo 14 0.96 8.73 0.55 7.63 8.30 8.65 9.17 10.03 ▃▇▆▅▂
delta_13_c_o_oo 13 0.96 -25.69 0.79 -27.02 -26.32 -25.83 -25.06 -23.79 ▆▇▅▅▂
year 0 1.00 2008.03 0.82 2007.00 2007.00 2008.00 2009.00 2009.00 ▇▁▇▁▇

At this early stage, it’s helpful to assess whether your dataset meets your expectations. Consider if the data appear as anticipated. Are the values in each column reasonable? Are there any noticeable gaps or errors that might need to be corrected, or that could potentially render the data unusable?

Your turn

The dataset has rows (including the headers) and 17 columns.

It also provides information on the type of data in each column

  • <chr> - means character or text data

  • <dbl> - means numerical data

Q Based on our summary functions are any variables assigned to the wrong data type (should be character when numeric or vice versa)?

Although some columns like date might not be correctly treated as character variables, they are not strictly numeric either, all other columns appear correct

Q Based on our summary functions do we have complete data for all variables?

No, they are 2 missing data points for body measurements (culmen, flipper, body mass), 11 missing data points for sex, 13/14 missing data points for blood isotopes (Delta N/C) and 290 missing data points for comments

We have just learned some ways to initially inspect our dataset. Keep in mind, we don’t expect everything to be perfect. This initial inspection is a good opportunity to identify where these issues might be and assess their severity.

When you are confident that the dataset is largely as expected, you are ready to start summarising your data.

16.4 Summary counts

In the previous section, we learned how to get an overview of our data’s structure, including the number of rows, the columns present, and any missing data. In this section, we will focus on summarising the data. Summarising data can provide insight into the scope and variation in our dataset, and help in evaluating its suitability for our analysis.

With our data we can count the total number of occurrences for different groups either by:

16.4.1 Filtering

penguins |> 
  filter(species == "Adelie") |> 
  count()
n
152

16.4.2 Grouping

Or by grouping :

penguins |> 
  group_by(species) |> 
  count()
species n
Adelie 152
Chinstrap 68
Gentoo 124

At this stage, these counts tell us what is in our dataset, not how variables relate to one another. To understand relationships, we will later need visualisations and models.

16.5 Frequency counts by subgroups

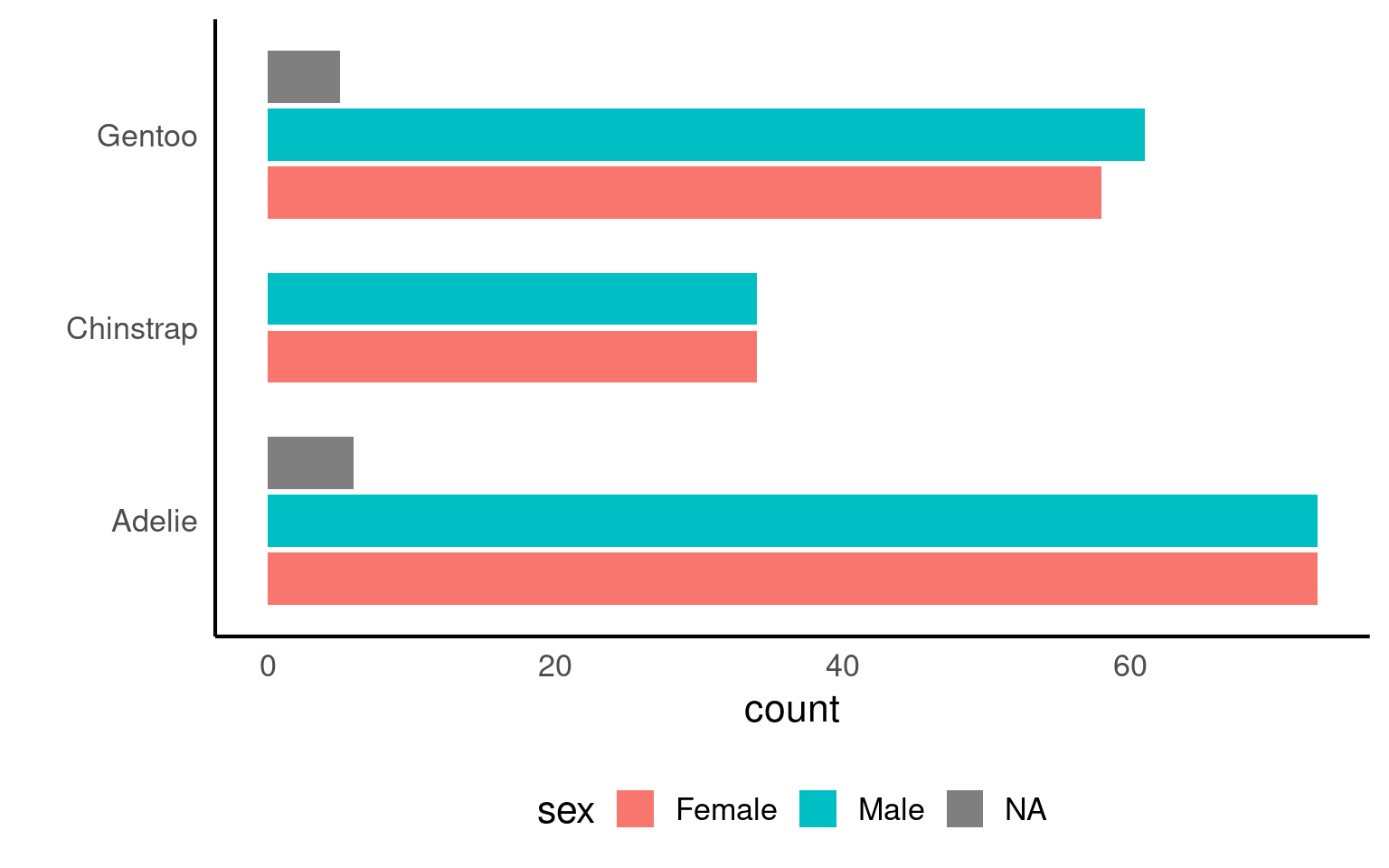
We can apply multiple grouping parameters at the same time - for example if we wish to know the frequency of observations by species and sex.

We can do this using dplyr or with functions in the janitor package:

penguins |> 
  group_by(species,sex) |> 
  count() |> 
  arrange(desc(n))
species sex n
Adelie Female 73
Adelie Male 73
Gentoo Male 61
Gentoo Female 58
Chinstrap Female 34
Chinstrap Male 34
Adelie NA 6
Gentoo NA 5 
penguins |>
  tabyl(sex, species) |> 
  adorn_percentages("all") |>
  adorn_totals(c("row", "col")) |>
  adorn_pct_formatting(digits = 1)
sex Adelie Chinstrap Gentoo Total
Female 21.2% 9.9% 16.9% 48.0%
Male 21.2% 9.9% 17.7% 48.8%
NA 1.7% 0.0% 1.5% 3.2%
Total 44.2% 19.8% 36.0% 100.0%

Grouped summaries implicitly assume that differences between groups may matter. Later, we will see that ignoring important grouping variables can lead to misleading conclusions

16.6 Visualising Frequencies

Graphs make summaries easier to interpret at a glance.

geom_col by default plots single values or “identity”, so numbers must be pre-calculated

penguins |> 
  group_by(species,sex) |> 
  count() |> 
  arrange(desc(n)) |> 
  ggplot(aes(x = species,
             y = n,
             fill = sex))+
  geom_col(position=position_dodge2(preserve="single"))+
  coord_flip()+
  labs(x = "")+
  theme(legend.position = "bottom")

penguins |> 
  group_by(species,sex) |> 
  count() |> 
  arrange(desc(n)) |> 
  ggplot(aes(x = species,
             y = n,
             fill = sex))+
  geom_col(position=position_dodge2(preserve="single"))+
  geom_label(aes(label = n),
             position=position_dodge2(preserve="single",
                                      width = .9))+ #<- dodge the text and label bars
  coord_flip()+
  labs(x = "")+
  theme(legend.position = "bottom")

geom_bar by default will summarise

penguins |> 
  ggplot(aes(x = species,
             fill = sex))+
  geom_bar(position=position_dodge2(preserve="single"))+
  coord_flip()+
  labs(x = "")+
  theme(legend.position = "bottom")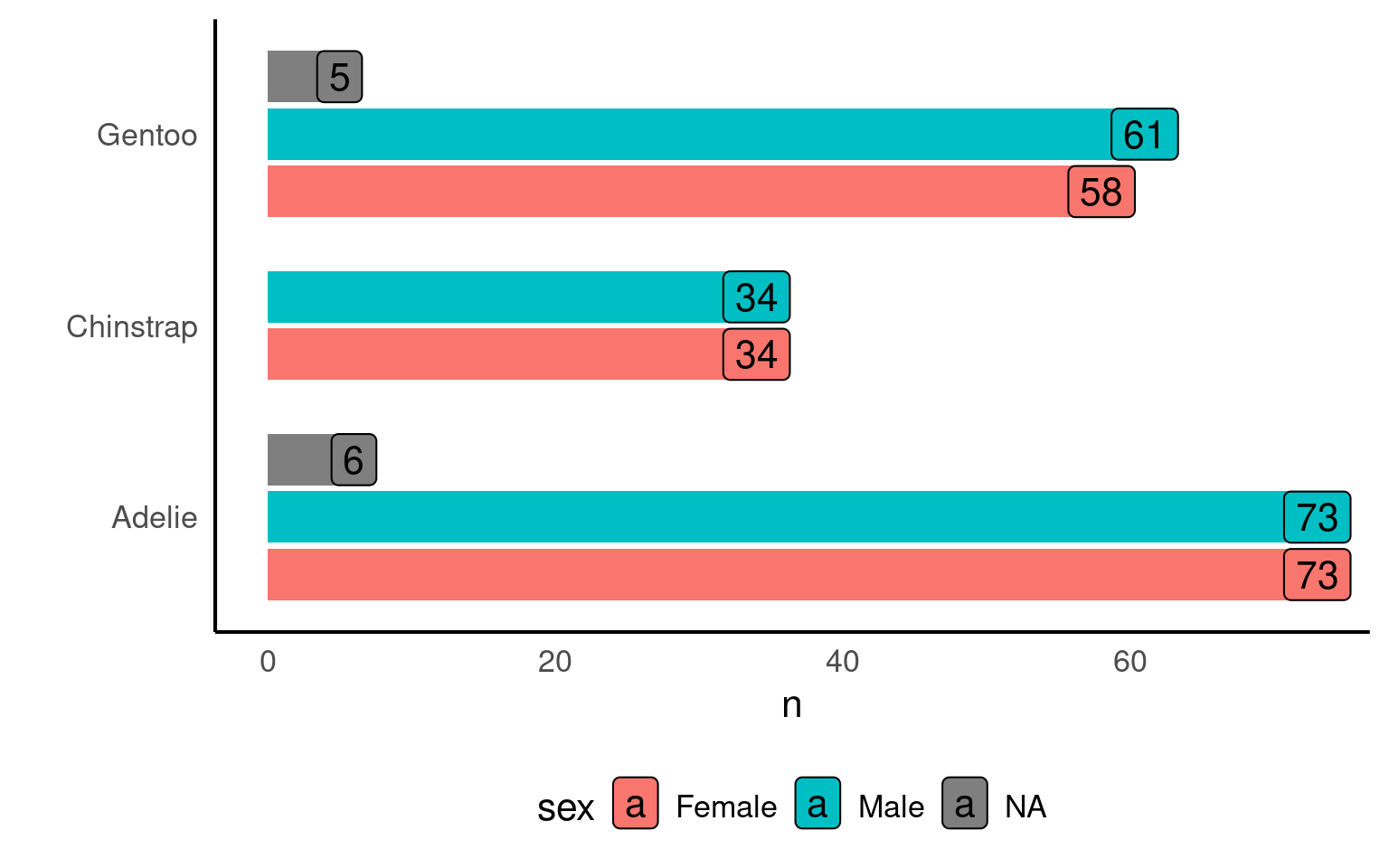

16.7 Exploring relationships between two variables

So far, we have focused on understanding the structure of the dataset and summarising individual variables or groups of observations. In many analyses, however, we are interested in how two variables vary together.

Exploring relationships between variables is an important step before modelling. At this stage, our goal is not to explain or predict outcomes, but to identify patterns, assess whether variables appear related, and consider whether these relationships differ across meaningful groups.

Plots are particularly important here, as numerical summaries alone can obscure important structure in the data.

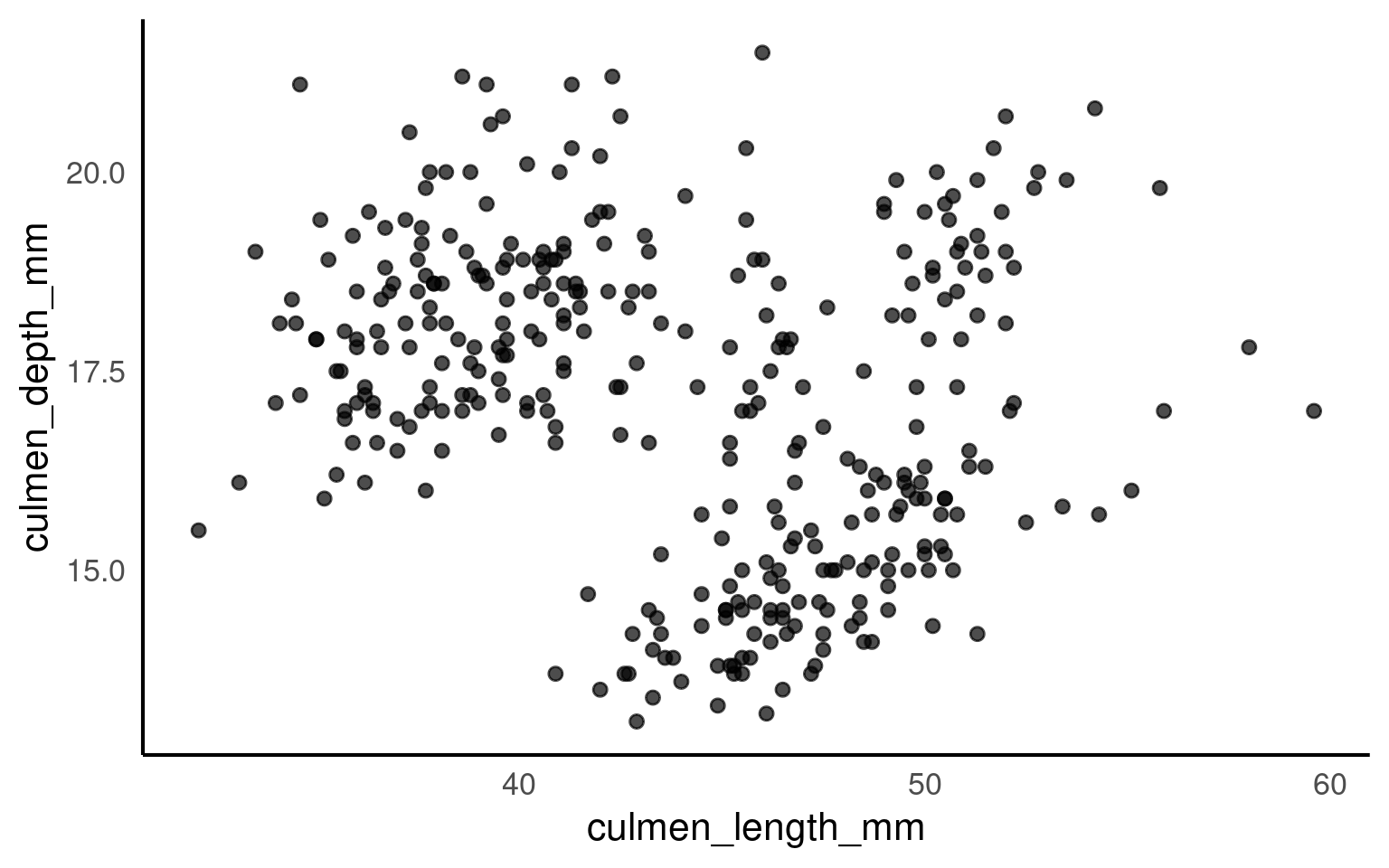
16.7.1 Scatterplots

When both variables of interest are numeric, a scatterplot is the most informative first tool. Scatterplots allow us to see how values of one variable change in relation to another and whether any patterns are present.

penguins|>
ggplot(aes(x = culmen_length_mm,
           y = culmen_depth_mm)) +
geom_point(alpha = 0.7)

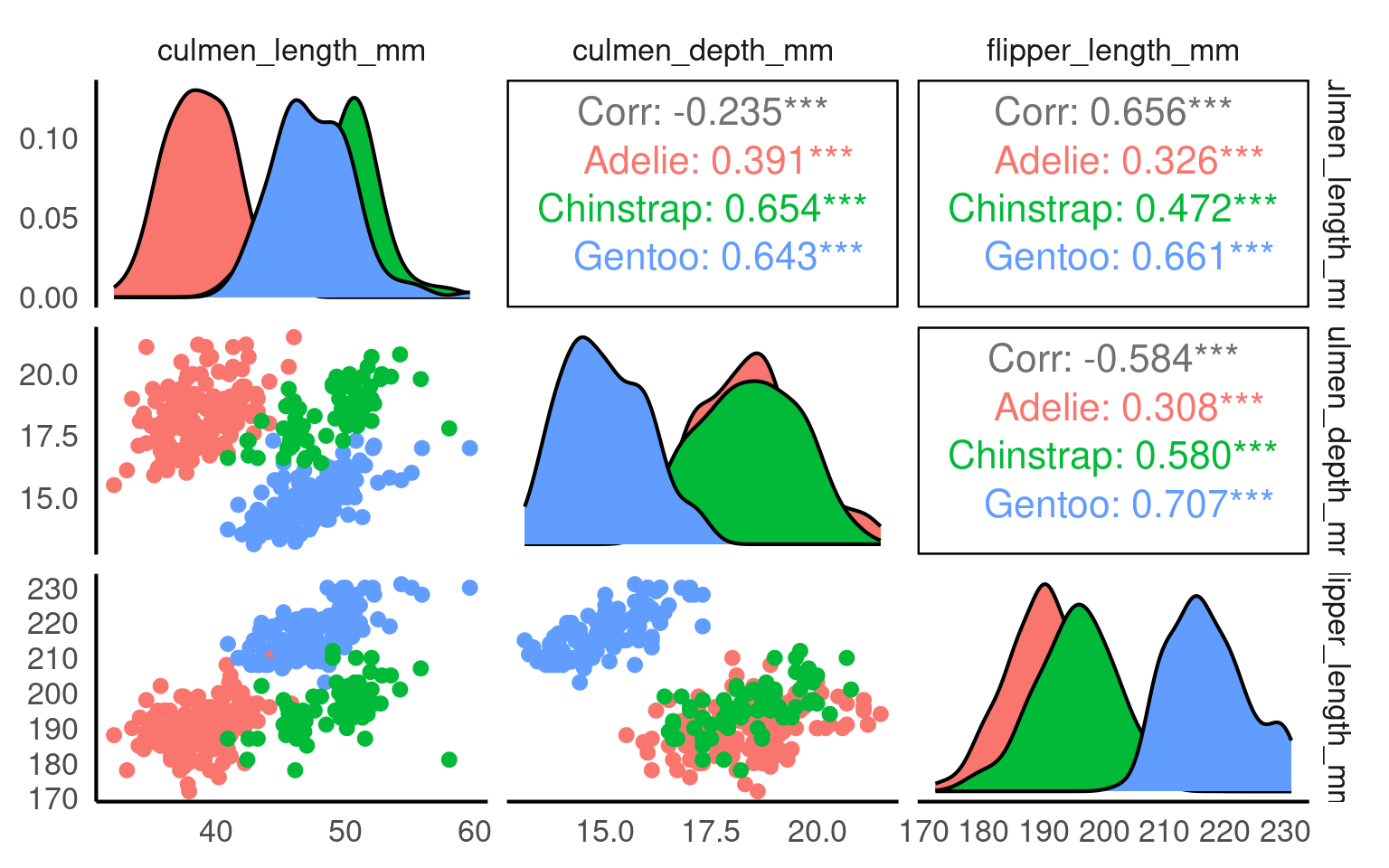
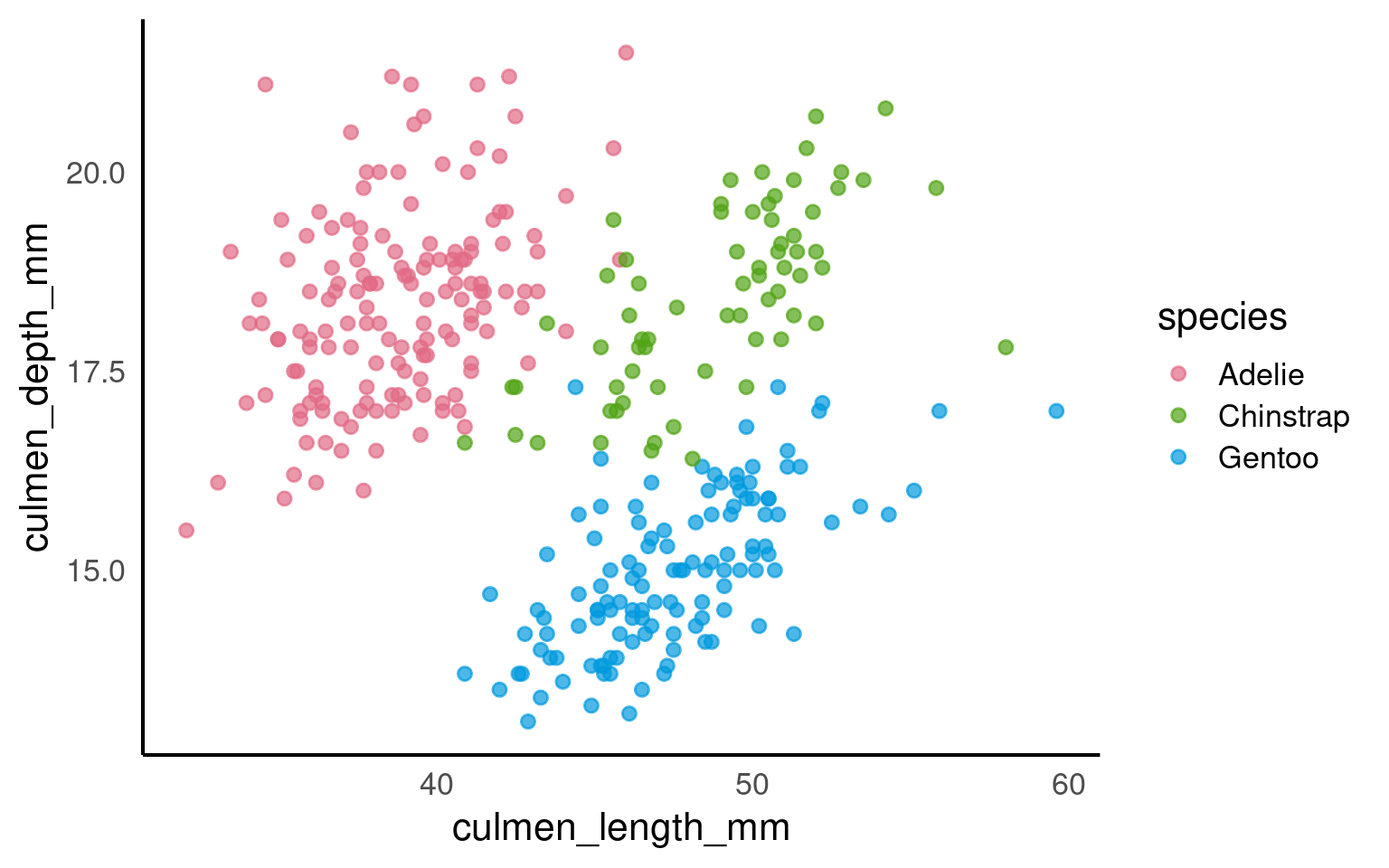
This plot shows the relationship between culmen length and culmen depth, with points coloured by penguin species.

Scatterplots such as this allow us to consider questions such as:

  • Do the variables appear positively or negatively associated?

  • Is the relationship approximately linear?

At this stage, we focus on visual comparison, rather than numerical summaries.

Your turn

Based on the scatterplot above, can you make a plot that includes species as an important grouping variable?

How does this change your observation?

penguins|>
ggplot(aes(x = culmen_length_mm,
           y = culmen_depth_mm,
           colour = species)) +
geom_point(alpha = 0.7)+
scale_colour_discrete_qualitative()

We now see a striking reversal of the apparent association between culmen length and depth, demonstrating the importance of considering groups in our analysis.

16.8 Correlation

In some situations, it can be useful to summarise the relationship between two numeric variables using a single numerical measure. Correlation provides such a summary by describing the strength and direction of a linear association between two variables.

Below, we calculate the overall correlation between culmen length and culmen depth across all observations.

penguins |>
summarise(
r = cor(culmen_length_mm,
        culmen_depth_mm,
use = "complete.obs") # Important to include if there are any missing values
)
r
-0.2350529

Your turn

How can we generate summary statistics that reflect our important subgrouping (species)?

How does this change your observation?

penguins |>
  group_by(species) |> 
summarise(
r = cor(culmen_length_mm,
        culmen_depth_mm,
use = "complete.obs") # Important to include if there are any missing values
)
species r
Adelie 0.3914917
Chinstrap 0.6535362
Gentoo 0.6433839

16.9 Summary statistics

We can extend our summaries to show not just counts, but also measures of central tendency (mean) and spread (standard deviation).

These are powerful ways to understand variation within groups. These summaries describe average differences, but they do not tell us whether one variable predicts another, nor whether relationships differ across groups.

penguins |>
group_by(species) |> # Calculate withing groups
summarise(
mean_mass = mean(body_mass_g, na.rm = TRUE),
sd_mass = sd(body_mass_g, na.rm = TRUE),
n = n(),
median = median(body_mass_g, na.rm = TRUE),
iqr = IQR(body_mass_g, na.rm = TRUE)
)
species mean_mass sd_mass n median iqr
Adelie 3700.662 458.5661 152 3700 650.0
Chinstrap 3733.088 384.3351 68 3700 462.5
Gentoo 5076.016 504.1162 124 5000 800.0

Your turn

penguins |>
group_by(species, sex) |> 
drop_na(sex) |> # Optional remove rows where Sex is unknown
summarise(
mean_mass_g = mean(body_mass_g, na.rm = TRUE),
sd_mass_g = sd(body_mass_g, na.rm = TRUE),
n = n()
)
species sex mean_mass_g sd_mass_g n
Adelie Female 3368.836 269.3801 73
Adelie Male 4043.493 346.8116 73
Chinstrap Female 3527.206 285.3339 34
Chinstrap Male 3938.971 362.1376 34
Gentoo Female 4679.741 281.5783 58
Gentoo Male 5484.836 313.1586 61

16.9.1 Summarise multiple variables

These functions allow us to generate

  • summarise_at()

Summarise specific selected variables:

penguins |> 
  group_by(species) |> 
  summarise_at(c("flipper_length_mm",
                 "culmen_length_mm",
                 "culmen_depth_mm"),
               mean, na.rm =T) # mean function
species flipper_length_mm culmen_length_mm culmen_depth_mm
Adelie 189.9536 38.79139 18.34636
Chinstrap 195.8235 48.83382 18.42059
Gentoo 217.1870 47.50488 14.98211
  • summarise_if()
penguins |> 
  group_by(species) |> 
  summarise_if(is.numeric, # selects only numeric columns
               mean, na.rm =T)
species sample_number culmen_length_mm culmen_depth_mm flipper_length_mm body_mass_g delta_15_n_o_oo delta_13_c_o_oo year
Adelie 76.5 38.79139 18.34636 189.9536 3700.662 8.859733 -25.80419 2008.013
Chinstrap 34.5 48.83382 18.42059 195.8235 3733.088 9.356155 -24.54654 2007.971
Gentoo 62.5 47.50488 14.98211 217.1870 5076.016 8.245338 -26.18530 2008.081

16.10 Visualising distributions

Numerical summaries such as the mean and standard deviation provide useful information about a variable, but they do not show the full distribution of values.

Visualising distributions allows us to see how values are spread, whether observations are concentrated in particular ranges, and how distributions differ across groups.

Different plots are suited to different questions. In this section, we focus on choosing appropriate plots for comparing distributions across groups.

16.10.1 Boxplots for group comparisons

A boxplot provides a compact summary of the distribution of a numeric variable. It displays the median, the spread of the central values, and potential extreme observations, making it particularly useful for comparing distributions between groups.

Below, we visualise the distribution of body mass across penguin species.

penguins |>
ggplot(aes(x = species,
           y = body_mass_g)) +
geom_boxplot() +
coord_flip()

This plot allows us to compare:

  • Median body mass across species,

  • IQR (the interquartile range) the spread of values within each species,

  • Whether some species show more variability than others.

Boxplots are especially effective when the primary goal is comparison between groups, rather than detailed inspection of the distribution shape.

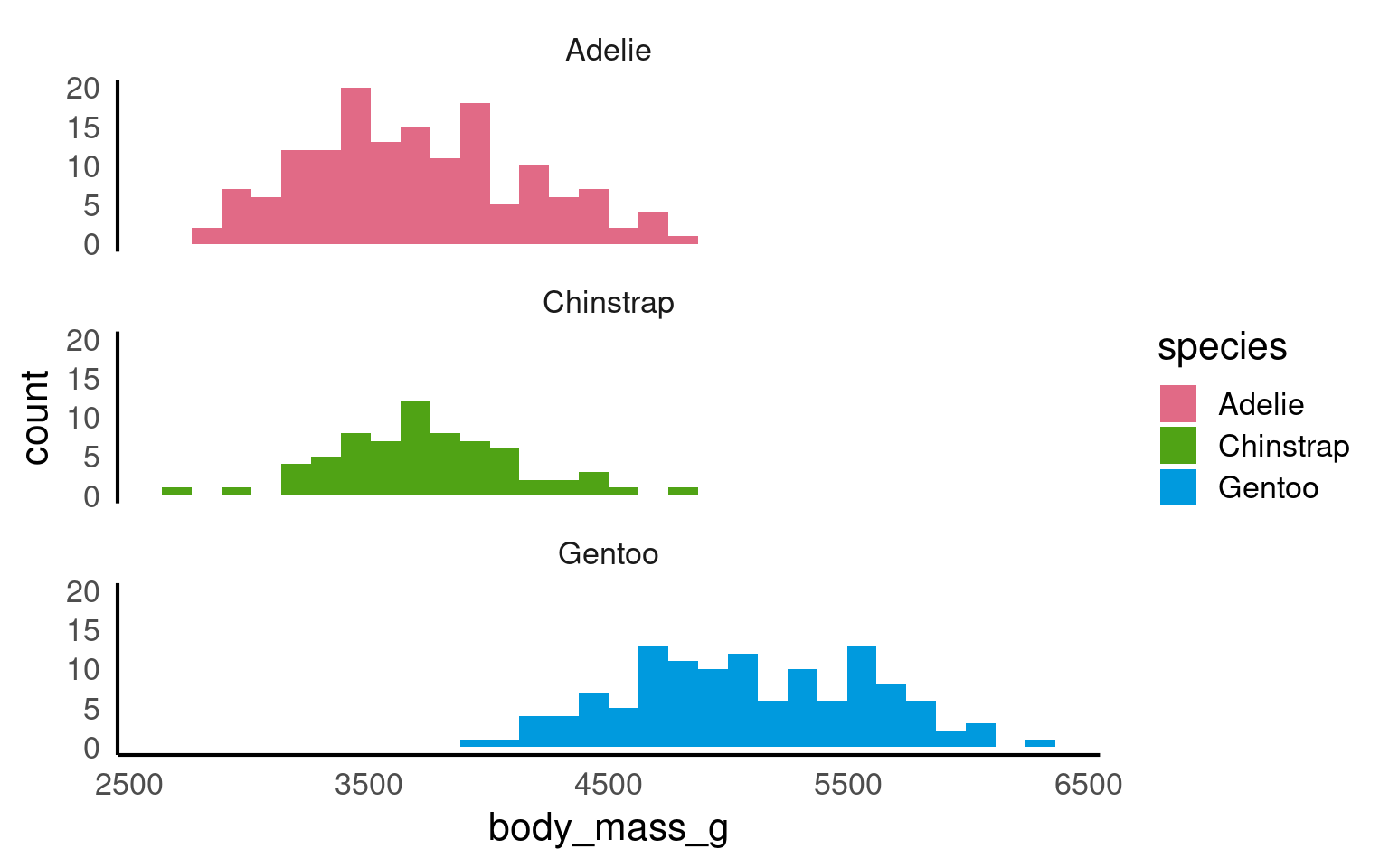
When visualising distributions, the choice of plot depends on the question being asked. In some cases, we are interested in comparing groups; in others, we want to explore the shape of the distribution within a single group.

Your turn

You are exploring body mass in the penguin dataset.

If you wanted to explore the shape of the body-mass distribution for each single species, how would you change the plot? (Hint: consider changing the geom rather than the data.)

A histogram could be used by changing the geom to geom_histogram() and focusing on one species, as this allows closer inspection of the distribution shape within that group.

penguins |> 
  ggplot(aes(body_mass_g,
             fill = species))+
  geom_histogram()+
  scale_fill_discrete_qualitative()+
  facet_wrap(~species, # make facets by species
             ncol = 1) # stack the plots for easier comparison

16.11 Useful summary functions

16.11.0.1 Measure of location:

  • mean(x): sum of x divided by the length

  • median(x): 50% of x is above and 50% is below

16.11.0.2 Measure of variation:

  • sd(x): standard deviation

  • IQR(x): interquartile range (robust equivalent of sd when outliers are present in the data)

16.11.0.3 Measure of rank:

  • min(x): minimum value of x

  • max(x): maximum value of x

  • quantile(x, 0.25): 25% of x is below this value

16.11.0.4 Counts:

  • n(x): the number of element in x

  • sum(!is.na(x)): count non-missing values

  • n_distinct(x): count the number of unique value

16.12 GGally

GGally is an invaluable tool in a researcher’s toolkit. It seamlessly extends the capabilities of the widely used ggplot2 package. With GGally, you can effortlessly create a variety of visualizations to explore and understand distributions and correlations among your variables. Its flexibility and ease of use make it a go-to choice for streamlining the process of creating insightful plots and charts for data analysis.

library(GGally)
penguins |> 
  select(species, island, culmen_length_mm, culmen_depth_mm, flipper_length_mm, body_mass_g, sex) |> 
  ggpairs()

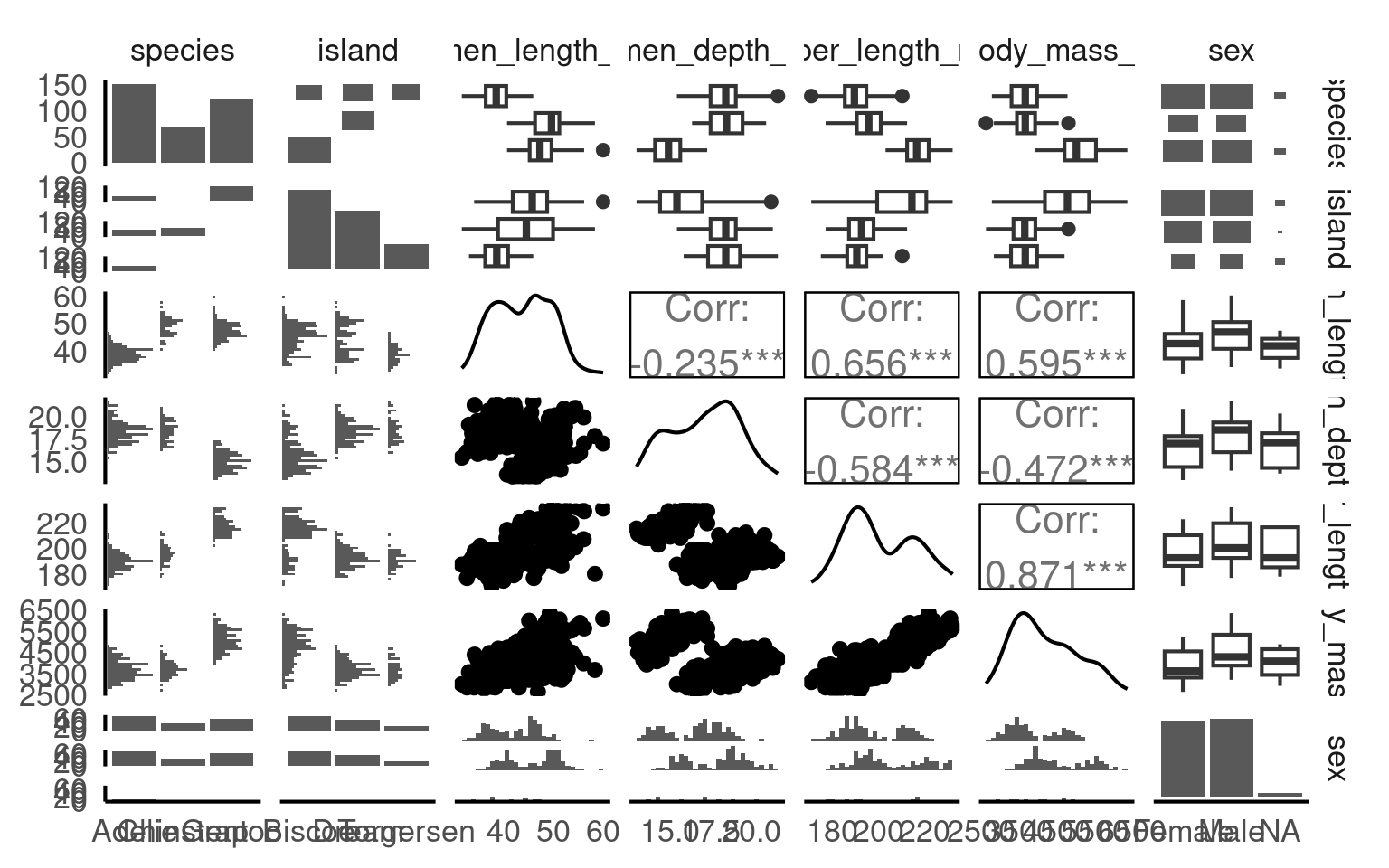
If we want to focus our exploration or include important grouping variables then this is also supported.

penguins |> 
  ggpairs(columns = 10:12, ggplot2::aes(colour = species))

16.13 Summary

In this section we learned to:

  • Inspect structure and completeness

    • Use glimpse(), str(), and skim() to understand column types, missing data, and variable ranges.

    • Confirm that variables are stored in appropriate formats (e.g. numeric vs character).

  • Summarise counts and categories

    Count observations using count() and group_by() to explore dataset composition.

    Use janitor::tabyl() for fast, readable cross-tabulations and percentages.

  • Calculate descriptive statistics

    • Compute group-wise summaries with summarise() such as means, SDs, and counts.

  • Visualise descriptive ranges and associations

    • Use ggplot to produce a range of descriptive plots