6 Worked Example 3 - Complex Designs
This is definitely the most complicated experiment we will analyse in this workbook, as a result of the complex data hierarchy.
6.1 The data
The BIODEPTH (Biodiversity and Ecosystem Process in Terrestrial Herbaceous Ecosystems) project manipulated grassland plant diversity in field plots to simulate the impact of the loss of plant species on ecosystem processes here above ground yield.
There is a gradient of managed species diversity with five levels ranging from monoculture to an attempted maximum for each site. This was repeated at eight different grassland sites across seven countries.
Each level of diversity was repeated with different mixtures of plant species chosen at random, and this is designed to separate the features of diversity from the species composition.
Experiments were repeated in two blocks per site.
biodepth <- read_tsv("files/Biodepth.txt")
biodepth <- biodepth %>%
mutate(Mix = factor(Mix),
Diversity2 = log(Diversity, 2)) %>%
drop_na()
# set Mix as a factor
# Set Diversity to log, base 2
head(biodepth)| Plot | Site | Block | Mix | Mix_Nested | Diversity | Shoot2 | Shoot3 | Diversity2 |
|---|---|---|---|---|---|---|---|---|
| B1P001 | Germany | A | 5 | 5 | 1 | 463.75 | 554.75 | 0 |
| B1P003 | Germany | A | 15 | 15 | 2 | 674.55 | 539.95 | 1 |
| B1P004 | Germany | A | 7 | 7 | 1 | 563.40 | 476.00 | 0 |
| B1P005 | Germany | A | 16 | 16 | 2 | 567.10 | 308.45 | 1 |
| B1P006 | Germany | A | 8 | 8 | 1 | 378.20 | 447.10 | 0 |
| B1P008 | Germany | A | 13 | 13 | 2 | 889.15 | 825.10 | 1 |
Important variables are:
Shoot2as one of the variables representing yield, our response or dependent variable.Diversity2Species richness indicator (on a log base 2 scale)Block,Site,Mixare all random effects
What follows is a complex design, but will hopefully outline the careful thought that must go into designing mixed-models
Q. Discussion - what is wrong with this design?
bio.lmer1 <- lmer(Shoot2 ~ Diversity2 + (1|Site) + (1|Block) + (1|Mix), data = biodepth)
summary(bio.lmer1)## Linear mixed model fit by REML. t-tests use Satterthwaite's method [
## lmerModLmerTest]
## Formula: Shoot2 ~ Diversity2 + (1 | Site) + (1 | Block) + (1 | Mix)
## Data: biodepth
##
## REML criterion at convergence: 6082.6
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -2.2187 -0.5179 -0.1031 0.3941 3.1735
##
## Random effects:
## Groups Name Variance Std.Dev.
## Mix (Intercept) 33665.3 183.48
## Block (Intercept) 383.2 19.57
## Site (Intercept) 30163.9 173.68
## Residual 22039.8 148.46
## Number of obs: 451, groups: Mix, 192; Block, 15; Site, 8
##
## Fixed effects:
## Estimate Std. Error df t value Pr(>|t|)
## (Intercept) 349.488 66.244 8.576 5.276 0.000598 ***
## Diversity2 78.901 12.059 175.159 6.543 6.42e-10 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Correlation of Fixed Effects:
## (Intr)
## Diversity2 -0.286Overall, the model assumes that the response variable "Shoot2" is influenced by the fixed effect "Diversity2" while accounting for the random effects due to the varying levels of "Site," "Block," and "Mix" within the data.
It also suffers from the fact that the design may be nested or crossed, it is not explicit. Basically we know that each block exists only within each site, they should be nested. If each block has a unique code then this is ok, but if for example they are coded as Germany: A/B, Switzerland A/B etc... then we would need to make our design explicity e.g. Site/Block.
This model also does not allow for any random slopes, which we may wish to consider.
Q. Discuss these two designs
bio.lmer1a <- lmer(Shoot2 ~ Diversity2 + (Diversity2 | Site) + (1 | Site/Mix) + (1 | Block), data = biodepth)
#Site/Mix denotes that Mix is nested fully within Site
bio.lmer2 <- lmer(Shoot2 ~ Diversity2 + (Diversity2|Site) + (1 | Site:Mix) + (1|Mix) + (1 | Block), data = biodepth)
# Site:Mix denotes the random effect varies independently for each combination of levels in the Site and Mix factorsIn the above designs we have produced a random slope and intercept for the effect of Site. This makes sense if we think that the way diversity affects yield may vary in a random site-specific manner.
What about the nesting or interaction of Site and Mix?
In the 1 | Site/Mix specification represents a nested random effect structure. It suggests that the random effect of Mix is nested within the random effect of Site. This specification assumes that the levels of Mix are nested within each level of Site, meaning that each level of Site has its own set of random effects for the levels of Mix. The / operator denotes the nesting relationship.
On the other hand 1 | Site:Mix specification, the random effect is specified as a two-way crossed random effect. It means that the random effect varies independently for each combination of levels in the Site and Mix factors. The : operator represents the interaction or crossed effect between the two factors. This specification allows for correlations between random effects within each combination of Site and Mix.
To summarize:
1 | Site:Mix: Two-way crossed random effect, allowing for independent variation of random effects for each combination of levels in Site and Mix.
1 | Site/Mix: Nested random effect, with the random effect of Mix nested within the random effect of Site, assuming that the levels of Mix are completely nested within each level of Site.
bio.lmer3 <- lmer(Shoot2 ~ Diversity2 + (Diversity2|Site) + (1 | Site:Mix) + (1|Mix), data = biodepth)
anova(bio.lmer2, bio.lmer3)| npar | AIC | BIC | logLik | deviance | Chisq | Df | Pr(>Chisq) | |
|---|---|---|---|---|---|---|---|---|
| bio.lmer3 | 8 | 6080.019 | 6112.911 | -3032.010 | 6064.019 | NA | NA | NA |
| bio.lmer2 | 9 | 6080.168 | 6117.171 | -3031.084 | 6062.168 | 1.851387 | 1 | 0.1736222 |
Q. What does the LRT indicate about the effect of block on our model?
Should we remove it from our model?
The LRT indicates that removing block from the design of our model does not produce a simpler model that explains significantly less variance. So in effect we could remove it. However, I would argue it also does not harm the model and it is part of our explicit design, so should be left in.
6.1.1 Model predictions
nested_data <- biodepth %>%
group_by(Site) %>%
nest()
models <- map(nested_data$data, ~ lm(Shoot2 ~ Diversity2, data = .)) %>%
map(predict)
biodepth.2 <- biodepth %>%
mutate(fit.m = predict(bio.lmer2, re.form = NA),
fit.c = predict(bio.lmer2, re.form = ~(1+Diversity2|Site)),
fit.l = unlist(models))
biodepth.2 %>%
ggplot(aes(x = Diversity2, y = Shoot2, colour = Site)) +
geom_point(pch = 16) +
geom_line(aes(y = fit.l), color = "black")+
geom_line(aes(y = fit.c))+
geom_line(aes(y = fit.m), colour = "grey",
linetype = "dashed")+
facet_wrap( ~ Site)+
coord_cartesian(ylim = c(0, 1200))+
theme(legend.position = "none")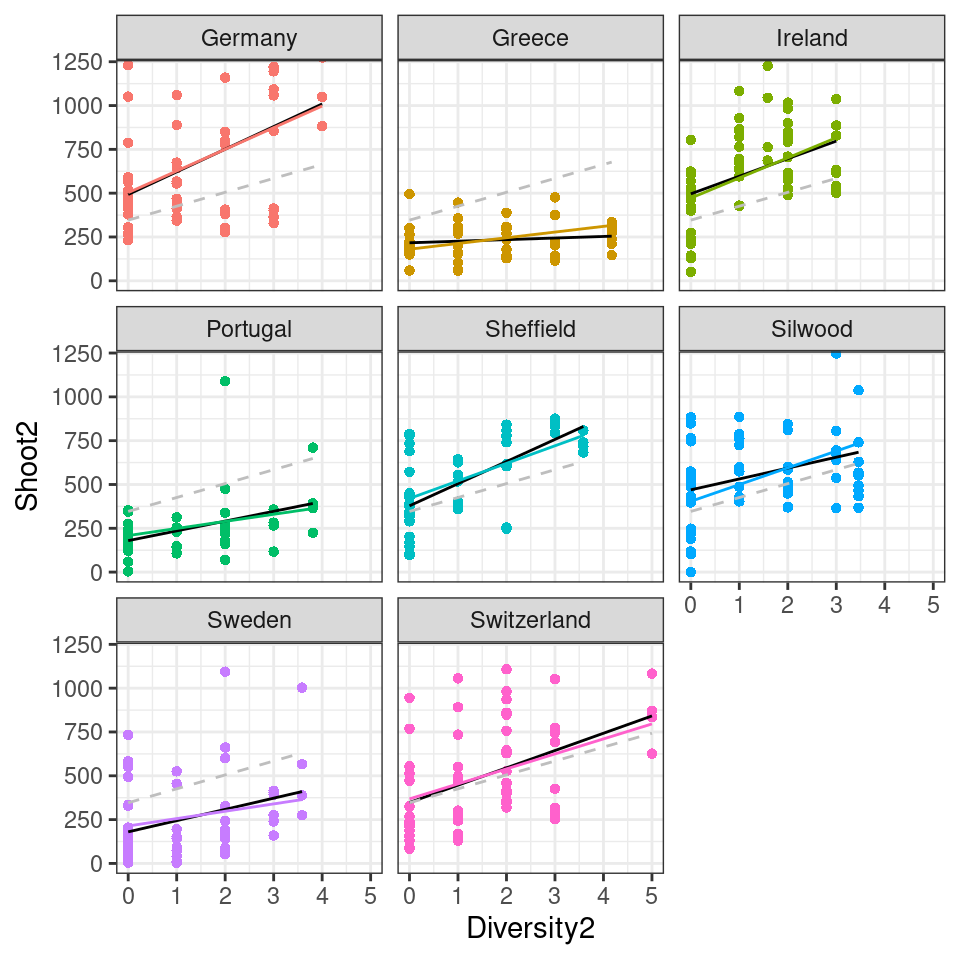
Q. Can you observe the effect of partial pooling in this analysis?