5 Types of Random Effects
5.1 Random slopes
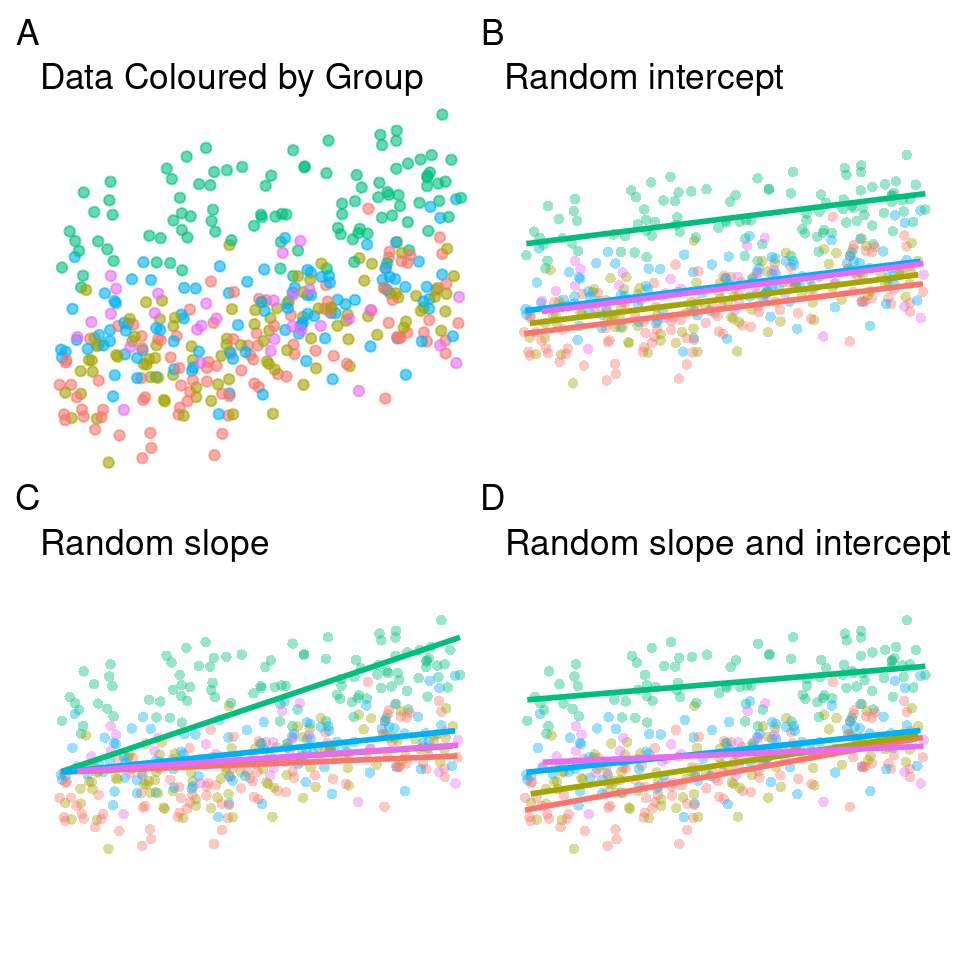
So far we have looked at random effects where each group has its own intercept. This means that we fit a regression line across all five groups, which has a constant slope but is allowed to shift up or down for each group. This is what is represented in panel B.
An alternative to the random intercepts model is the random slopes model, shown in panel C. In this model the slopes are permitted to vary, but the intercept is fixed across all groups. For our current data the random slopes model does a fair job as well.
Finally we can allow both the intercepts and slope to vary between groups, as shown in panel D. This captures both the shallower slope of some of our groups and the vertical offsets present. If you inspect the original data set we generated, you can see that the random effect for group was calculated as both a product of random distribution on the intercept and slope, so it is not surprising that here this model fits the data best.
This model will use more degrees of freedom than the other two, as these must be used to calculate variance for both intercept and slope.
# random intercept model
lmer1 <- lmer(y ~ x + (1|group), data = data)
plot_function(lmer1, "Random intercept")
# Random slope model
lmer2 <- lmer(y ~ x + (0 + x | group), data = data)
plot_function(lmer2, "Random slope")
# Random slope and intercept model
lmer3 <- lmer(y ~ x + (x | group), data = data)Mixed-effects models are enormously flexible. The decision about whether to include random intercepts, random slopes, or both will depend heavily on your hypotheses. It is generally quite rare to see random slopes models only, and more commonly it will be a question of whether random intercepts or random intercepts and random slopes are necessary.
As the combine random slopes and intercept model requries more degrees of freedom, it may be the case that using likelihood ratio tests (LRT) are advisable to decide which model describes the data best (more on this later).
Because random intercepts models require fewer degrees of freedome, these may be easier to fit when data sets have fewer observations.
In a random effects model, the random effects are assumed to be a random sample from a population of possible random effects. These random effects capture the variation between different groups or clusters in the data. The number of random effects is typically smaller than the total number of observations, as the random effects represent the distinct groups or clusters in the dataset.
The degrees of freedom associated with the random effects in a linear mixed model reflect the number of independent groups or clusters in the data, rather than the number of individual observations. For example, if you have data from 100 individuals, but they belong to only 10 distinct groups, the random effects would have 10 degrees of freedom, not 100.
By using fewer degrees of freedom for the random effects, the model accounts for the fact that the group-level variation is estimated based on a smaller number of parameters. This approach helps prevent overfitting and provides a more appropriate estimation of the variance components associated with the random effects.
5.2 Model refining / Likelihood Ratio Tests
Once we have produce an initial model with a random effects structure, we may wish to perform model selection by comparing different nested models with varying random effects structures. It allows us to assess whether the inclusion of additional random effects or changes in the random effects structure significantly improve the model fit. By comparing the likelihood values of different nested models, we can determine which model provides a better fit to the data.
Previously we looked at the random intercepts vs. random intercepts and slopes model and concluded that the latter looked like it fit the data best.
We can use a likelihood ratio test with the anova() function if we want to determine if the fit is significantly different to the simpler randome intercepts only model.
anova(lmer1, lmer3)| npar | AIC | BIC | logLik | deviance | Chisq | Df | Pr(>Chisq) | |
|---|---|---|---|---|---|---|---|---|
| lmer1 | 4 | 3236.091 | 3252.347 | -1614.046 | 3228.091 | NA | NA | NA |
| lmer3 | 6 | 3228.442 | 3252.825 | -1608.221 | 3216.442 | 11.64947 | 2 | 0.0029536 |
There is a literature on the idea of model selection, that is, an automated (or sometimes manual) way of testing many versions of a model with a different subset of the predictors in an attempt to find the model that fits best. These are sometimes called “stepwise” procedures.
Others argue this method has a number of flaws, including:
-
Doing this is basically “p-value mining”, that is, running a lot of tests till you find a p-value you like.
-
Your likelihood of making a false positive is very high.
-
Adding/removing a new variable can have an effect on other predictors.
Instead of doing model selection, you should use your knowledge of the data to select a subset of the variables which are either a) of importance to you, or b) theoretically influential on the outcome. Then you can fit a single model including all of this.
However, I would argue that while the inclusion of random effects and their structure should have a clear rationale before implementation, adjustments to better understand the best type of random effects structure is perfectly reasonable.
5.2.1 Maximum Likelihood
Frequentist fit used by LMM through lme4 / lmer is based on the Maximum Likelihood principle, where we maximize the likelihood \(L(y)\) of observing the data \(y\), which is equivalent to minimizing residuals of the model, the Ordinary Least Squares (OLS) approach. It measures the probability of observing the data given a specific set of parameter values.
When we are attempting to optimise a model we can use the likelihood ratio test (LRT). Given two nested models, denoted as Model 1 and Model 2, the LRT compares the likelihood values of these models to assess whether the more complex Model 2 provides a significantly better fit to the data compared to the simpler Model 1. The LRT statistic, denoted as \(D\), is calculated as the difference between the log-likelihood values of Model 1 and Model 2, multiplied by 2:
\[D = -2~*~(ln(L_1)-ln(L_2))\]
Here \(L_1\) represents the likelihood value of Model 1, and \(L_2\) represents the likelihood value of Model 2. The LRT statistic follows a chi-square (\(\chi^2\)) distribution with degrees of freedom equal to the difference in the number of parameters between the two models.
To determine the statistical significance of the LRT statistic, one can compare it to the critical value from the chi-square distribution with the appropriate degrees of freedom. If the LRT statistic exceeds the critical value, it indicates that the more complex Model 2 provides a significantly better fit to the data compared to the simpler Model 1.
ML estimation is often used to perform hypothesis tests, including the chi-square test. The chi-square test compares the observed data to the expected data predicted by a statistical model. It assesses the goodness-of-fit between the observed data and the model's predictions.
5.2.2 REML
REML (Restricted Maximum Likelihood) estimation is a variant of ML estimation that addresses the issue of bias in the estimation of random effects in mixed effects models. In mixed effects models, random effects account for the variation at the group or individual level that is not explained by the fixed effects. However, the inclusion of random effects introduces a bias in the ML estimates, as they are influenced by the variability of the random effects.
REML estimation addresses this bias by optimizing the likelihood function conditional on the fixed effects only, effectively removing the influence of the random effects on the estimation. This approach provides unbiased estimates of the fixed effects and is especially useful when the primary interest lies in the fixed effects rather than the random effects.
5.2.3 ML vs. REML fitting
Maximum Likelihood (ML) estimation is preferable when comparing nested models because it allows for the direct comparison of the likelihood values between different models. ML estimation provides a quantitative measure of how well a given model fits the observed data, based on the likelihood function.
In this context, ML estimation is preferable because it allows for a formal statistical comparison between nested models. It provides a rigorous and objective way to assess whether the inclusion of additional parameters in the more complex model leads to a significantly better fit to the data compared to the simpler model. This approach ensures that model comparisons are based on sound statistical principles and helps in determining the most appropriate model for the given data.
REML can be preferable when producing unbiased estimates of the fixed effects. Older versions of model fitting packages like lmer used to require the manual switch between REML and ML when fitting models in order to switch between the objectives of assessing goodness-of-fit and interpreting estimates. But you will notice that when you perform an LRT with the anova() function it informs you the switch is being made automatically.